前端技术
HTML
CSS
Javascript
前端框架和UI库
VUE
ReactJS
AngularJS
JQuery
NodeJS
JSON
Element-UI
Bootstrap
Material UI
服务端和客户端
Java
Python
PHP
Golang
Scala
Kotlin
Groovy
Ruby
Lua
.net
c#
c++
后端WEB和工程框架
SpringBoot
SpringCloud
Struts2
MyBatis
Hibernate
Tornado
Beego
Go-Spring
Go Gin
Go Iris
Dubbo
HessianRPC
Maven
Gradle
数据库
MySQL
Oracle
Mongo
中间件与web容器
Redis
MemCache
Etcd
Cassandra
Kafka
RabbitMQ
RocketMQ
ActiveMQ
Nacos
Consul
Tomcat
Nginx
Netty
大数据技术
Hive
Impala
ClickHouse
DorisDB
Greenplum
PostgreSQL
HBase
Kylin
Hadoop
Apache Pig
ZooKeeper
SeaTunnel
Sqoop
Datax
Flink
Spark
Mahout
数据搜索与日志
ElasticSearch
Apache Lucene
Apache Solr
Kibana
Logstash
数据可视化与OLAP
Apache Atlas
Superset
Saiku
Tesseract
系统与容器
Linux
Shell
Docker
Kubernetes
站内搜索
用于搜索本网站内部文章,支持栏目切换。
名词解释
作为当前文章的名词解释,仅对当前文章有效。
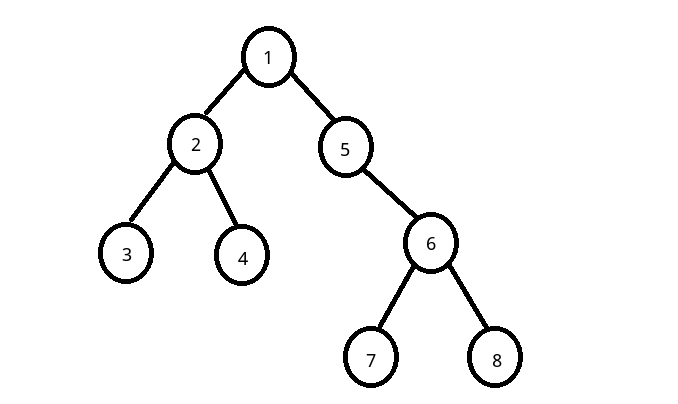
最近公共祖先(Lowest Common Ancestor, LCA):在计算机科学中,特别是在树或图的数据结构中,最近公共祖先是指在一棵有根树中,对于任意两个节点x和y,它们的最近公共祖先是指深度最大的一个节点,这个节点同时位于从根节点到节点x和节点y的路径上。例如,在文章中的实例中,节点3和节点6的最近公共祖先为节点1,因为节点1是它们各自路径上的最深的共同节点。
倍增算法:倍增算法是一种利用二进制思想进行优化搜索的技术,它通常用于减少查询次数以提高算法效率。在解决LCA问题时,通过预处理构建一个路径数组,使得可以在O(logn)的时间复杂度内快速确定节点向上跳指定步数后的祖先节点。在信息学竞赛场景下,倍增法求解LCA问题的核心在于对树的深度进行二进制拆分,从而实现快速定位最近公共祖先。
并查集(Disjoint-Set Union, DSU):并查集是一种用于维护一组不相交集合的数据结构,常用于处理合并与查找集合间关系的问题。在Tarjan版LCA算法中,并查集用于记录树中各个节点之间的父子关系,便于在遍历过程中快速判断节点间的包含关系以及合并集合。当需要查找两个节点x和y的最近公共祖先时,可以通过遍历树节点并结合并查集操作来确定它们的最近公共祖先节点。
延伸阅读
作为当前文章的延伸阅读,仅对当前文章有效。
在深入探讨了LCA(最近公共祖先)问题的两种主流解决算法——倍增法与Tarjan版LCA之后,我们可以进一步关注这一理论在实际应用中的最新进展与相关研究动态。在数据结构和算法领域,LCA问题不仅被广泛应用于信息学竞赛中,还在计算机科学诸多分支,如图论、数据库索引设计、网络路由优化等方面发挥着重要作用。
近年来,随着大数据和人工智能技术的发展,处理大规模图数据的需求日益增强,对LCA问题求解效率的要求也随之提高。例如,在社交网络分析中,寻找两个用户的最近共同好友或社群,实质上就是一种LCA问题的应用;而在基因组学中,比对不同物种间的进化关系时,利用改进的LCA算法能更高效地定位序列的共同祖先节点。
2021年,一项发表在《ACM Transactions on Algorithms》的研究中,科研人员提出了一种基于预处理和动态规划相结合的新型LCA算法,能够在保持较低空间复杂度的同时,进一步提升查询速度,为大规模图数据处理提供了新的解决方案。同时,针对并查集在求解LCA问题上的局限性,也有学者提出了更为精细的设计策略,通过引入路径压缩与按秩合并等优化手段,使得经典Tarjan算法在处理特定类型的数据时,性能得到显著改善。
总之,LCA问题作为基础算法研究的重要组成部分,其理论发展与实践应用的紧密结合,将持续推动信息技术的进步,并在更多新兴领域产生深远影响。不断涌现的创新研究成果,正持续拓宽我们对LCA问题理解的深度和广度,也为未来算法设计与优化指明了方向。
近年来,随着大数据和人工智能技术的发展,处理大规模图数据的需求日益增强,对LCA问题求解效率的要求也随之提高。例如,在社交网络分析中,寻找两个用户的最近共同好友或社群,实质上就是一种LCA问题的应用;而在基因组学中,比对不同物种间的进化关系时,利用改进的LCA算法能更高效地定位序列的共同祖先节点。
2021年,一项发表在《ACM Transactions on Algorithms》的研究中,科研人员提出了一种基于预处理和动态规划相结合的新型LCA算法,能够在保持较低空间复杂度的同时,进一步提升查询速度,为大规模图数据处理提供了新的解决方案。同时,针对并查集在求解LCA问题上的局限性,也有学者提出了更为精细的设计策略,通过引入路径压缩与按秩合并等优化手段,使得经典Tarjan算法在处理特定类型的数据时,性能得到显著改善。
总之,LCA问题作为基础算法研究的重要组成部分,其理论发展与实践应用的紧密结合,将持续推动信息技术的进步,并在更多新兴领域产生深远影响。不断涌现的创新研究成果,正持续拓宽我们对LCA问题理解的深度和广度,也为未来算法设计与优化指明了方向。
知识学习
实践的时候请根据实际情况谨慎操作。
随机学习一条linux命令:
groups user
- 显示指定用户的所属组。
推荐内容
推荐本栏目内的其它文章,看看还有哪些文章让你感兴趣。
2023-02-18
2023-08-07
2023-09-10
2024-01-12
2023-01-11
2023-10-22
2023-01-13
2023-10-29
2024-01-09
2023-08-26
2023-01-02
2023-05-10
历史内容
快速导航到对应月份的历史文章列表。
随便看看
拉到页底了吧,随便看看还有哪些文章你可能感兴趣。
时光飞逝
"流光容易把人抛,红了樱桃,绿了芭蕉。"